Aotle

你所看到的惊鸿，都曾被平庸磨练

Aotle

动态规划入门，也算是考试复习⑧

跳台阶

题目描述

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

输入

多组测试样例。每组测试样例包含一个整数n。(1<=n<=100)

输出

每组测试样例输出一行，表示青蛙跳上n级台阶的跳法数量.

所得到的结果模1000000007

样例输入

1
2
3
4

样例输出

1
2
3
5

思路

动态规划 dp[n]=dp[n-1]+dp[n-2] 跳到第n阶的方法等于跳到第n-1阶再跳一次加上跳到第n-2阶再跳两阶。dp[1]=1;dp[0]=1;dp[2]=2;

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include <bits/stdc++.h>
using namespace std;
//动态规划入门题，跳台阶
int dp[105];
int n;
int main()
{
    dp[0] = 1;
    dp[1] = 1;
    dp[2] = 2;
    for (int i = 3; i < 100;++i){
        dp[i] = (dp[i - 1] + dp[i - 2]) % 1000000007;
    }
    while(cin>>n){
        cout << dp[n] << endl;
    }
}

打家劫舍

题目描述

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
示例 1：

输入：[1,2,3,1]
输出：4
解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
     偷窃到的最高金额 = 1 + 3 = 4 。
示例 2：

输入：[2,7,9,3,1]
输出：12
解释：偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
     偷窃到的最高金额 = 2 + 9 + 1 = 12 。
提示：

0 <= nums.length <= 100
0 <= nums[i] <= 400

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/house-robber

思路

动态规划 ，偷最后一间，最大金额等于前面max dp[n-2]+最后一间 ，偷倒数第二间就等于max dp[n-1]；

https://leetcode-cn.com/problems/house-robber/solution/dong-tai-gui-hua-jie-ti-si-bu-zou-xiang-jie-cjavap/

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <bits/stdc++.h>
using namespace std;
int dp[105];
int n;
int rob(vector<int>& nums) {
    if(nums.size()==0)
        return 0;
    dp[1] = nums[0];
    dp[0] = 0;
    for (int i = 2; i <= nums.size();++i){
        dp[i] = max(dp[i - 2] + nums[i-1], dp[i - 1]);
    }
    return dp[nums.size()];
}
int main()
{
    int n;
    cin >> n;
    vector<int> a(n,0);

    for (int i = 0; i < n;++i){
        cin >> a[i];
    }
    cout << rob(a) << endl;
    return 0;
}

买卖股票的最佳时机

题目描述

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

如果你最多只允许完成一笔交易（即买入和卖出一支股票一次），设计一个算法来计算你所能获取的最大利润。

注意：你不能在买入股票前卖出股票。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock

输入输出

1
2
3
4
5
6
7
8
9
10
11
示例 1:

输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。
示例 2:

输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

思路

最低点买入 ，最低点后面的最高点卖出。记录每个区间的最大值的最大值。动态规划

代码

1
2
3
4
5
6
7
8
9
10
11
12
int maxProfit(vector<int>& prices) {
    if(prices.size()<=1){
        return 0;
    }
    int maxl = 0;
    int minl = 10000000;
    for (int i = 0; i < prices.size();++i){
        maxl = max(maxl, prices[i] - minl);
        minl = min(minl, prices[i]);
    }
    return maxl;
}

最大子段和

题目描述

给定n个整数组成的序列a1,a2,…an, 求子段和ai+ai+1+…+aj（子段可为空集）的最大值。

输入

包含多组测试数据。第一行为一个整数T(1<=T<=20)，代表测试数据个数。

每组测试数据第一行为一个整数n，代表有n个整数(1<=n<=10000)。

接下来一行有n个数x(-1000<=x<=1000)。

输出

输出其对应的最大子段和。

样例输入

1
2
3
1
6
2 -11 4 13 -1 2

样例输出

1
18

提示

子段可为空集，答案为0

思路

前面的和大于0，则加上，小于0则抛弃

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <bits/stdc++.h>
using namespace std;
int dp[10005];
int s[10005];
int n;

int main()
{
    int t;
    cin >> t;
    while(t--){
        cin >> n;
        int sum=0x80000000;
        for (int i = 0; i < n;++i){
            cin >> s[i];
            if(dp[i]>0)
                dp[i + 1] = dp[i] + s[i];
                else
                    dp[i + 1] = s[i];
                sum = max(dp[i + 1], sum);
        }
        cout << sum;
    }
    return 0;
}

最长公共子序列

题目描述

给你一个序列X和另一个序列Z，当Z中的所有元素都在X中存在，并且在X中的下标顺序是严格递增的，那么就把Z叫做X的子序列。
例如：Z=<a,b,f,c>是序列X=<a,b,c,f,b,c>的一个子序列，Z中的元素在X中的下标序列为<1,2,4,6>。
现给你两个序列X和Y，请问它们的最长公共子序列的长度是多少？

输入

输入包含多组测试数据。每组输入占一行，为两个字符串，由若干个空格分隔。每个字符串的长度不超过100。

输出

对于每组输入，输出两个字符串的最长公共子序列的长度。

样例输入

1
2
3
abcfbc abfcab
programming contest 
abcd mnp

样例输出

1
2
3
4
2
0

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <bits/stdc++.h>
using namespace std;
int dp[105][105] = {0};
char s[105];
char s1[105];
int n;

int main()
{
    while(cin>>s>>s1){
        for (int i = 1; i <= strlen(s);++i){
            for (int j = 1; j <= strlen(s1);++j){
                if(s[i-1]==s1[j-1])
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                else
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
        cout << dp[strlen(s)][strlen(s1)] << endl;
    }
    return 0;
}

背包问题

题目描述

已知有N种物品和一个可容纳C重量的背包。每种物品i的重量为Wi，价值为Pi。那么，采用怎样的装包方法才会使装入背包物品的总价值最大。

输入

包含多组测试数据。第一行为一个整数T(1<=T<=10)，代表测试数据个数。

接下来有T组测试数据。每组测试数据第一行为背包的重量C(C<10000)和物品个数N(N<1000)。接下来的N行分别为物品的重量cost(1<=cost<=100)和价值val(1<=val<=3000000)。（注意：结果可能超过int范围）

输出

对每组测试数据，输出其对应的所装物品的最大价值。

样例输入

1
2
3
4
5
6
7
1
10 5
2 6
2 3
6 5
5 4
4 6

样例输出

1
15

思路

节约空间，用一维数组m[i]代表容量为i的时候可以装入的最大价值。

每一次V[i][j]改变的值只与V[i-1][x] {x:1...j}有关，V[i-1][x]是前一次i循环保存下来的值；因此，可以将V缩减成一维数组，从而达到优化空间的目的，状态转移方程转换为 m(j)= max{m(j), m(j-w(i))+v(i)}；

并且，状态转移方程，每一次推导V[i][j]是通过V[i-1][j-w(i]来推导的，所以一维数组中j的扫描顺序应该从大到小(capacity到0)，否者前一次循环保存下来的值将会被修改，从而造成错误。

img

img

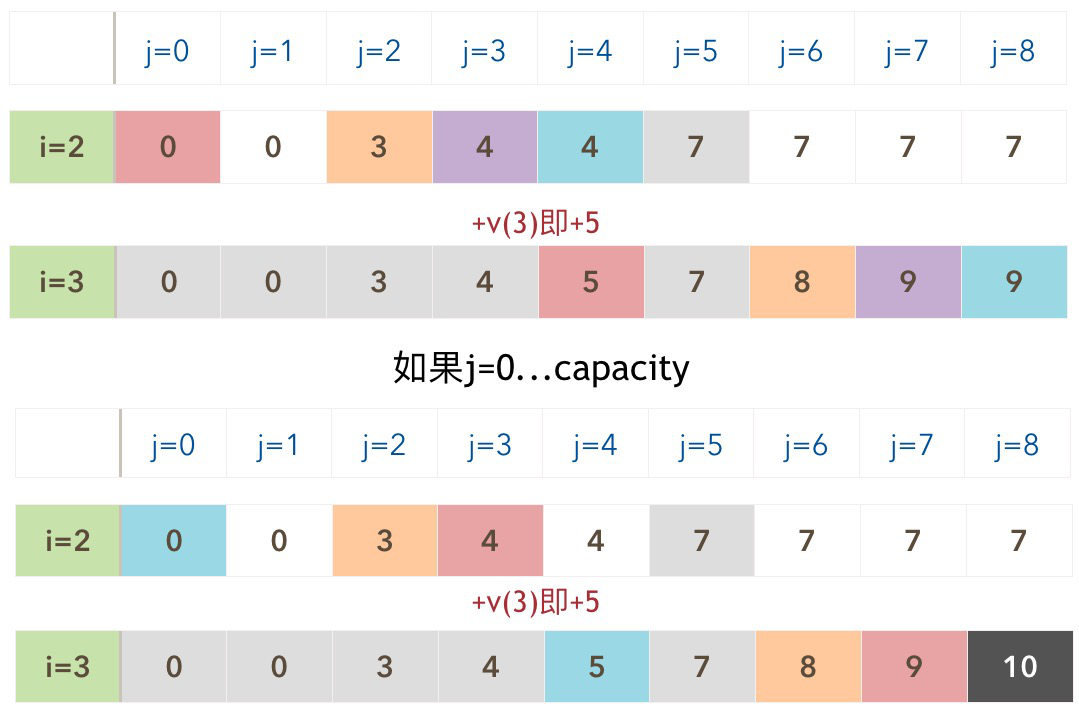
同样以上述例子中i=3时来说明，有:

1
2
3
4
5
6
7
8
9
10
11
　　　　1) i=3，j=8，w(3)=4，v(3)=5，有j>w(3)，则B(8)=max｛B(8)，B(8-w(3))+v(3)｝=max｛B(8)，B(4)+5｝=max｛7，4+5｝=9；

　　　　2) j- -即j=7，有j>w(3)，则B(7)=max｛B(7)，B(7-w(3))+v(3)｝=max｛B(7)，B(3)+5｝=max｛7，4+5｝=9；

　　　　3) j- -即j=6，有j>w(3)，则B(6)=max｛B(6)，B(6-w(3))+v(3)｝=max｛B(6)，B(2)+5｝=max｛7，3+5｝=8；

　　　　4) j- -即j=5，有j>w(3)，则B(5)=max｛B(5)，B(5-w(3))+v(3)｝=max｛B(5)，B(1)+5｝=max｛7，0+5｝=7；

　　　　5) j- -即j=4，有j＝w(3)，则B(4)=max｛B(4)，B(4-w(3))+v(3)｝=max｛B(4)，B(0)+5｝=max｛4，0+5｝=5；

　　　　6) j- -即j=3，有j<w(3)，继续访问数组会出现越界，所以本轮操作停止，B(0)到B(3)的值保留上轮循环（i=2时）的值不变，进入下一轮循环i++；

img

　　如果j不逆序而采用正序j=0…capacity，如上图所示，当j=8时应该有B(8)=B(8-w(3))+v(3)=B(4)+5，然而此时的B(4)已经在j=4的时候被修改过了，原来的B(4)=4，现在B(4)=5，所以计算得出B(8)=5+5=10，显然这于正确答案不符合；所以该一维数组后面的值需要前面的值进行运算再改动，如果正序便利，则前面的值将有可能被修改掉从而造成后面数据的错误；相反如果逆序遍历，先修改后面的数据再修改前面的数据，此种情况就不会出错了；

参考：https://www.cnblogs.com/christal-r/p/dynamic_programming.html

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <iostream>
using namespace std;
typedef long long ll;
const int maxn = 1005;
ll m[maxn][maxn];
int main()
{
    int t, n;
    ll c, w[maxn], v[maxn];
    scanf("%d", &t);
    //cin >> t;
    while (t--)
    {
        scanf("%lld %d", &c, &n);
        //cin >> c >> n;
        for (int i = 1; i <= n; i++)
        {
            scanf("%lld %lld", &w[i], &v[i]);
            //cin >> w[i] >> v[i];
        }
        int i,j,jMax = min(w[n] - 1, c);
        for (int j = 0; j <= jMax; j++)
            m[n][j] = 0;
        for (int j = w[n]; j <= c; j++)
            m[n][j] = v[n];
        for (int i = n - 1; i > 1; i--)
        {
            jMax = min(w[i] - 1, c);
            for (int j = 0; j <= jMax; j++)
                m[i][j] = m[i + 1][j];
            for (int j = w[i]; j <= c; j++)
                m[i][j] = max(m[i + 1][j], m[i + 1][j - w[i]] + v[i]);
        }
        m[1][c] = m[2][c];
        if (c >= w[1])
            m[1][c] = max(m[1][c], m[2][c - w[1]] + v[1]);
        printf("%lld\n", m[1][c]);
        //cout << m[1][c] << endl;
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <iostream>
using namespace std;
typedef long long ll;
const int maxn = 1005;
ll m[10005];
int main()
{
    int t, n;
    ll c, w[maxn], v[maxn];
    scanf("%d", &t);
    //cin >> t;
    while (t--)
    {
        scanf("%lld %d", &c, &n);
        //cin >> c >> n;
        for (int i = 1; i <= n; i++)
        {
            scanf("%lld %lld", &w[i], &v[i]);
            //cin >> w[i] >> v[i];
        }
        for (int i = 1; i <= n;i++){
            for (int j = c; j >= 1;j--){
                if(m[j]<=m[j-w[i]]+v[i] && j-w[i]>=0 )//二维变一维，防止越界
                {
                   m[j]=m[j-w[i]]+v[i];
                }
            }
        }
        cout << m[c] << endl;
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include<iostream>
#include<vector>
using namespace std;

int main()
{
    int w, n;
    cin >> w >> n;
    vector<int> wei(1), val(1);
    for(int i = 0; i < n; i++)
    {
        int a, b;
        cin >> a >> b;
        wei.push_back(a);
        val.push_back(b);
    }
    vector<vector<int>> dp(n+1, vector<int>(w+1));

    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= w; j++)
        {
            if(wei[i] > j)
                dp[i][j] = dp[i-1][j];
            else
                dp[i][j] = max(dp[i-1][j-wei[i]]+val[i], dp[i-1][j]);
        }
    }
    cout << dp[n][w] << endl;
}

节食的限制

题目描述

Bessie像她的诸多姊妹一样，因為从Farmer John的草地吃了太多美味的草而长出了太多的赘肉。所以FJ将她置於一个及其严格的节食计划之中。她每天不能吃多过H(5<=H<=45000)公斤的乾草。Bessie只能吃一整綑乾草；当她开始吃一綑乾草的之后就再也停不下来了。她有一个完整的N(1<=n<=50)綑可以给她当作晚餐的乾草的清单。她自然想要尽量吃到更多的乾草。很自然地，每綑乾草只能被吃一次（即使在列表中相同的重量可能出现2次，但是这表示的是两綑乾草，其中每綑乾草最多只能被吃掉一次）。 给定一个列表表示每綑乾草的重量Si(1<=Si<=H),求Bessie不超过节食的限制的前提下可以吃掉多少乾草（注意一旦她开始吃一綑乾草就会把那一綑乾草全部吃完）。

输入

第一行：两个由空格隔开的整数：H和N， 第2到N+1行：第i+1行是一个单独的整数，表示第i綑乾草的重量Si。

输出

一个单独的整数表示Bessie在限制范围内最多可以吃多少公斤的乾草。

样例输入

1
2
3
4
5
56 4
15
19
20
21

样例输出

1
56

思路

重量和价值相等的0-1背包问题。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <iostream>
using namespace std;
typedef long long ll;
const int maxn = 55;
ll m[45005];
int main()
{
    int n;
    ll c, w[maxn];
        scanf("%lld %d", &c, &n);
        //cin >> c >> n;
        for (int i = 1; i <= n; i++)
        {
            scanf("%lld", &w[i]);
            //cin >> w[i] >> v[i];
        }
        for (int i = 1; i <= n;i++){
            for (int j = c; j >= 1;j--){
                if(m[j]<=m[j-w[i]]+w[i] && j-w[i]>=0 )//二维变一维
                {
                   m[j]=m[j-w[i]]+w[i];
                }
            }
        }
        cout << m[c] << endl;

    return 0;
}

汽车费用

题目描述

一个特别的单行街道在每公里处有一个汽车站。顾客根据他们乘坐汽车的公里使来付费。例如下表就是一个费用的单子。没有一辆车子行驶超过10公里，一个顾客打算行驶n公里(1<=n<100)，它可以通过无限次的换车来完成旅程。最后要求费用最少。

输入

第一行十个整数分别表示行走1到10公里的费用(<=500)。注意这些数并无实际的经济意义，即行驶10公里费用可能比行驶一公里少。第二行一个整数n表示，旅客的总路程数。

输出

仅一个整数表示最少费用。

样例输入

1
2
12 21 31 40 49 58 69 79 90 101
15

样例输出

1
147

思路

动态规划，依次计算出行走i公里需要的最少费用。

计算行走i公里最少费用时，用j遍历[1~i0]，当i>=j的时候依次比较m[i]和n[j]+m[i-j]的值，遍历完成后，m[i]为最少费用。

例如，m[4] = min(m[0]+n[4], m[1]+n[3], m[2]+n[2], m[3]+n[1])

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <iostream>
using namespace std;
typedef long long ll;
const int maxn = 0x7fffffff;
int m[105];
int n[15];
int main()
{
    for (int i = 1; i <= 10;++i){
        cin >> n[i];
    }
    int t;
    cin >> t;
    for (int i = 1; i <= t;i++){
        m[i] = maxn;
        for (int j = 1; j <= 10;j++){
            if(i>=j)
                m[i] = min(m[i], m[i - j] + n[j]);
        }
    }
    cout << m[t] << endl;
    return 0;
}

求数组的最长递减子序列

题目描述

给定一个整数序列，输出它的最长递减（注意不是“不递增”）子序列。

输入

输入包括两行，第一行包括一个正整数N（N<=1000），表示输入的整数序列的长度。第二行包括用空格分隔开的N个整数，整数范围区间为[-30000,30000]。

输出

输出最长递减子序列，数字之间有一个空格。

样例输入

1
2
8
9 4 3 2 5 4 3 2

样例输出

1
9 5 4 3 2

思路

O(nlogn)的写法，有点困了，明天起来再理解一下。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <bits/stdc++.h>
using namespace std;
int g[30010], num[30010], d[30010];
int main()
{
    int n;
    scanf("%d", &n);
    int inf = 0x7fffffff;
    fill(g, g + n, inf);
    for (int i = 0; i < n; ++i)
    {
        scanf("%d", &num[n - 1 - i]);
    }
    //核心代码begin
    //挺难理解的，不过确实很厉害
    for (int i = 0; i < n; ++i)
    {
        int j = lower_bound(g, g + n, num[i]) - g; //找到大于等于num[i]的第一个位置下标
        g[j] = num[i];                             //把num[i]放入g[j]的位置
        d[i] = j + 1;                              // 实际上放的就是每个元素为结尾的最大长度
    }
    //end
    int s = *max_element(d, d + n); //找到最大长度
    for (int i = n - 1; i >= 0; --i) //为什么从后向前遍历？因为最长子序列上一个序列一定是再这个字母前面的嘛 比如 4 3 2 1 -> 4是最后一个，3一定在4的前面
    {
        if (s == d[i])
        {
            if (s != 1)
                printf("%d ", num[i]);
            else
                printf("%d\n", num[i]);
            --s;
        }
    }
    return 0;
}

博客内容遵循 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 协议

本文永久链接是：http://aotle.top/2020/11/07/dongtaiguihua/

评论